Explaining the transmission speed limit for quantum entanglement RIKEN

Tomotake Kuhara, RIKEN Hakubei Research Team, RIKEN Hakubei Research Team for Quantum Complexity Analysis, RIKEN Quantum Computer Research Center (RIKEN Hakubei Research Team, RIKEN Hakubei Quantum Complexity Analysis, RIKEN Hakubei Research Team, Leading Research Division), Fu Fanten Special Joint Research Team led by SITREF With researcher and professor Keiji Saito from the Faculty of Science at Kyoto UniversityBose particle^[1]in the systemQuantum entanglement^[2]We have demonstrated theoretically the maximum transmission speed.

The results of this research provide new insights into understanding the quantum mechanical behavior resulting from the interaction of many Bose particles, and at the same time,Quantum computer^[3]It is expected that this research will also contribute to clarifying the fundamental limitations in information processing technology, including information processing technology.

For many years, the question of how quickly Bose particles, the fundamental particles seen in quantum mechanics, can transfer quantum information through interactions has remained unresolved.

Joint research teamReef Robinson limit^[4]We investigated a concept called ', and theoretically demonstrated the limits of the speed of information transmission.' As a result, another fundamental particlefermion^[5]It has been revealed that Bose particles, unlike Bose particles, cause a phenomenon called information transfer acceleration. Using this result, we simulated the interaction of Bose particles on a quantum computer.Guaranteed accuracy^[6]We have developed a new method.

This research was conducted in the scientific journalNature CommunicationsPublished in the online edition (March 21).

background

In quantum physics, invisible particles such as electrons and atoms play the main role, and the properties of matter are determined by how they interact with each other. A collection of these particles is called a “quantum many-body system,” and understanding this complex world has become an important topic in modern science, from the motion of electrons to superconductivity and the development of quantum computers.

However, the question of how fast quantum information can travel, or in other words, what is the “speed of sound” in the quantum world, has remained a mystery for a long time. This is where the concept of the Reeve-Robinson limit comes into play. In 1972, physicists Reeve and Robinson showed theoretically that there is a limit to the speed of information transmission in the quantum world, just as sound and radio waves travel at a constant speed in our universe.

This discovery advances fundamental understanding in many areas of quantum physics, including quantum information transfer, quantum entanglement propagation, quantum communications, and quantum computer design. For example, in a quantum computer, this limit can limit the speed at which information can be transferred between qubits. It also provides clues about how quantum entanglement propagates in order to understand temporal changes in quantum many-body systems.

The theory was originally innovative by Reeve and RobinsonQuantum rotation system^[7]Born from research. This theory has been applied to various quantum systems to improve our understanding of deep problems in quantum physics. Of particular interest are fermions and bosons, which are considered the most important in quantum mechanics. They have different statistical properties about the behavior of particles. Fermions can be treated in a similar way to quantum spin, but the nature of Bose particles means that an infinite number of them can exist in the same quantum state, so the approach to these particles is completely different.

Over the past 20 years, many researchers have continued to try to clarify the Reif-Robinson limit for Bose particle systems, and although many advances have been made, the problem has not been solved. Exploring the Reeve-Robinson limit is of great importance in quantum information science, from the fundamental theory of quantum mechanics to actual technological applications. Solving this puzzle is expected to be the key to understanding the quantum world and lead to future technological innovations.

Research methods and results

The biggest obstacle to clarifying the Reeve-Robinson limit in Bose particle systems is the possibility that huge amounts of energy can be released when Bose particles assume the same state. This property of Bose particles is:Superconductivity^[8]orSuper liquid^[9]、Bose-Einstein condensation^[10]This causes macroscopic quantum effects that can be seen with the naked eye.

In this paper we derive a new theory that addresses the Reeve-Robinson limit when there are no energy constraints, and explain two aspects of information transfer by Bose particle systems. The first thing we focused on was the moving speed of the Bose particle. The discovery here is that the Bose particle moves at a finite speed, meaning that there is an upper limit to its speed. It has been shown that there is no qualitative difference between fermions and bosons in this regard.

However, what is interesting is the part about the speed of transferring quantum information. Bose particles have special properties that allow many particles to be in the same state. As a result, they discovered that when information such as quantum entanglement is included, the speed of information transmission can increase in proportion to the number of particles. In other words, Bose particle clusters can enhance the ability to transmit information quickly. This discovery reveals a specific situation in which quantum entanglement transmission through Bose particles occurs in an accelerated manner.

Consider the following situation: Bose particles move one after another in a straight path. Over time, more and more Bose molecules accumulate along this path, and the density of the molecules increases. As this study revealed, the speed of information transfer is proportional to the particle density, indicating that information transfer accelerates as particle density increases. In other words, under certain conditions, information can be transmitted quickly by the way particles are packed together. However, even using this acceleration mechanism, we have obtained theoretical evidence that the speed of information transmission by Bose particles does not increase to infinity. This means that there is an upper limit to the transfer of information due to the laws of nature (Figure 1).

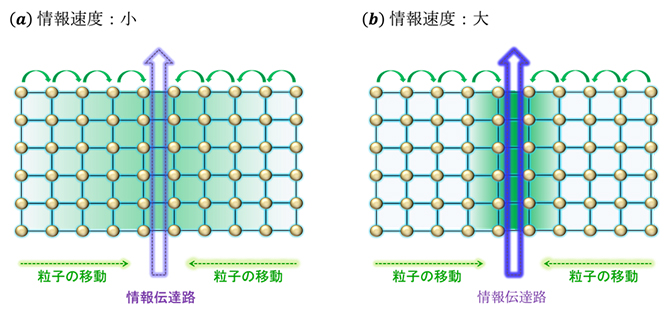
Figure 1: Schematic diagram of quantum entanglement propagation acceleration

It turns out that Bose particles move with a finite speed. They also revealed that when a large number of Bose particles gather in the same place, they each cooperate to speed up the transmission of quantum entanglement. This phenomenon means that focusing Bose particles on a specific information transmission path increases the speed of information transmission for this transmission path. For example, in the case where Bose particles are arranged on a two-dimensional grid, if the particle density in the central part is low (A), the transmission speed in that part will also be relatively small. However, if a large number of Bose particles are concentrated in center B, the transmission speed becomes large there.

This research revealed a previously unimaginable phenomenon: the rapid transfer of information. Traditionally, many scientists believe that information is transmitted at a constant rate in Bose particle systems, just as it is in fermion systems. This new discovery is counterintuitive. However, this study also indicates that although this acceleration phenomenon is theoretically possible, it is unlikely to occur in the real world. Under normal circumstances, information transmission still has a limited speed, as demonstrated by previous research that Conducted by the joint research team^NB). The concept discussed in this study, the Reeve-Robinson limit, is a theoretical framework that places a limit on the maximum possible speed of information transmission. To precisely understand this limit of Bose particle interactions, we must take into account all the propagation velocities under different conditions. One of the main reasons this problem has not been solved is that the interactions between Bose particles are so complex that it has been difficult to consider all possibilities. To address this problem, the joint research team theoretically predicted the conditions under which information would be transmitted most rapidly, and succeeded in proving mathematically that these conditions were indeed optimal. This result is an important step towards understanding complex particle interactions and delving deeper into the limits of information transfer.

As an application of this research, we have developed a new method for simulating interacting Bose particle systems on a quantum computer using the Reif-Robinson limit. In many-body quantum systems, many quantum mechanical particles interact in a complex way, and this is difficult to accurately and efficiently simulate using conventional computers. Quantum simulation technology plays an important role here. The joint research team focused on digital quantum simulation, which uses quantum computers to manipulate qubits to digitally mimic the quantum system of interest. This process requires time to divide it into parts and perform appropriate quantum operations in each period to imitate the motion of a Bose particle. The amount of entanglement produced, or the amount of entanglement that occurs over time, is key to determining the amount of quantum operations required. The Reeve-Robinson limit of the Bose particle system obtained in this study has allowed a quantitative assessment of the amount of quantum entanglement generated. As a result, a method was created to perform digital quantum simulations of Bose particles more efficiently while maintaining high accuracy. This development represents a major step forward in the field of quantum simulation and has the potential to expand the range of applications for the study of complex quantum systems and quantum computing.

• NB)Tomotaka Kuwahara and Keiji Saito, Constrained Leib Robinson and Quasilinear Light Cones in Boson Interaction, Physics of Systems. Fox. easy. 127, 070403 (2021)

Future expectations

In this study, we elucidate the limits to the propagation speed of quantum entanglement in Bose particle systems. In the future, important tasks will be to elucidate new physical phenomena resulting from accelerated information transfer and to clarify the Reif-Robinson limit when there are long-range interactions between Bose particles.

Supplementary explanation

• 1.Bose particle
  A quantum particle follows Bose-Einstein statistics and has an integer spin (the quantum number of angular momentum). This property allows multiple Bose particles to occupy the same quantum state simultaneously. Typical Bose particles include photons (particles of light), gluons (particles that mediate strong forces), and some atoms.
• 2.Quantum entanglement
  A phenomenon in which two or more particles are closely linked in their quantum states, which has the property that by measuring the state of one particle, the state of the other can be instantly determined. It has the property of transmitting information instantaneously regardless of distance, and plays an important role in quantum information technology and quantum computing.
• 3.Quantum computer
  A computer works on a completely different principle than traditional computers. While classical computers use bits (0 or 1) as the basic unit of information, quantum computers use quantum bits (qubits). By exploiting quantum entanglement, it is possible to perform calculations much faster than with conventional computers.
• 4.Reef Robinson limit
  It represents the critical speed of information transfer in a many-body quantum system. It was introduced in 1972 by Elliot Reeve and Derek Robinson. This speed depends on the physical properties of the system and the strength of interactions, and constitutes a fundamental constraint on entanglement and the non-local propagation of information.
• 5.fermion
  A particle whose spin is half an integer (1/2, 3/2…) and follows the Pauli exclusion principle. According to this principle, no two fermions can exist in the same quantum state. Electrons, protons, and neutrons are examples of fermions. The properties of fermions are important in explaining many physical phenomena, such as the arrangement of electrons within atoms and the electrical properties of solids.
• 6.Guaranteed accuracy
  It is known that errors generally exist in quantum calculations. Accuracy assurance refers to the methodology of quantitatively evaluating this error and obtaining highly reliable computational results.
• 7.Quantum rotation system
  In quantum mechanics, a collection of particles with intrinsic angular momentum is called spin.
• 8.Superconductivity
  It is a phenomenon in which electrical resistance becomes completely zero when a particular material is cooled to a very low temperature, allowing current to flow without loss.
• 9.Super liquid
  This is a quantum mechanical phenomenon that occurs when liquid helium is cooled to extremely low temperatures, in which case the liquid loses its viscosity and behaves as if there were no internal friction.
• 10.Bose-Einstein condensation
  When Bose particles are cooled to extremely low temperatures, the effects of quantum mechanics become observable at the macroscopic level, causing many particles to “condense” into the lowest energy state and share the same quantum state.

Research support

This research is supported by the Japan Society for the Promotion of Science (JSPS) Scholarship for Young Investigators 'Computational Complexity Analysis of Quantum Many-Body Problems Using Tensor Network Format (Principal Investigator: Tomotake Kuwabara)' and the Japan Science and Technology Agency (JSPS). This work was supported by the Strategic Innovative Research Promotion (JST) project “Development of High-Speed ​​Algorithms for Quantum Computers Using Quantum Many-Body Theory (Research Representative: Tomotake Kuhara, JPMJPR2116)''.

Original paper information

• Tomotaka Kuhara, Tan Fan Fu, and Keiji Saito, “Effective light cone and numerical quantum simulation of interacting bosons,” Nature Communications, 10.1038/s41467-024-46501-7

Presenter

Ricken
Quantum Computer Research Center Quantum Complexity Analysis Riken Hakobe Research Team
Riken Hakubei, leader of the research team, Tomotaka Kuhara
(RIKEN Hakubei Research Team Leader, Kawahara Quantum Complexity Analysis, Riken Hakubei Research Team, Research Headquarters)
Private researcher Fu Van Tan

Faculty of Science, Kyoto University
Professor Keiji Saito

Tomotake Kuwahara

Fu Bangtan

Keiji Saito

Press attaché

Public Relations Office RIKEN Press Office
Inquiry form

Kyoto University, Department of External Public Relations, Office of International Public Relations
Tel: 075-753-5729 / Fax: 075-753-2094
Email: comms [at] mail2.adm.kyoto-u.ac.jp

※[at]Please replace with @.

Inquiry regarding industrial use

Inquiry form